Дискретные распределения (Alatissa эксперт по теории вероятности)

Если кому интересно, то покажу таблицу, когда экспоненциальные записи я уже перевела в десятичные
Выглядеть это будет вот так

Далее, я сделаю расчеты, когда значения функции распределения 14 знаков после запятой
и будет более понятно, что это за значения
т.е экселевские автомат.  расчеты меня как-то не очень устроили)



Далее, для каких целей расчитывается фр
На какие вопросы можно ответить, когда есть расчеты функции распределения и плотности вероятности

на самом деле экселевские расчеты норм, просто очень округленные.
 

...

   

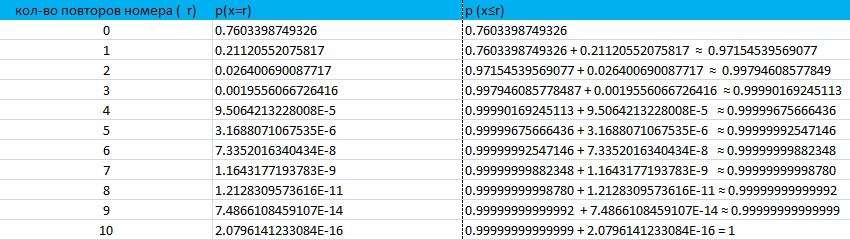
Все, кто внимательно посмотрел на столбик с расчетами интегр функции, то поняли, что они из себя представляют:
f(0)= p(0)
f(1) = p(0) + p(1)
f(2) = p(0) + p(1) + p(2)
f(3) = p(0) + p(1) + p(2) + p(3)
f(4) = p(0) + p(1) + p(2) + p(3) + p(4)
f(5) = p(0) + p(1) + p(2) + p(3) + p(4) + p(5)
и т.д.

Т.е идет суммирование вероятностей, и с каждым разом все ближе и ближе к единице.

 p(0) + p(1) + p(2) + p(3) + p(4) + p(5) + p(6) + p(7) + p( + p(9) + p(10) = 1

Поэтому в автомат. расчетах будут часто встечаться много единиц в значениях интегральной фр, это просто очень сильно приближенные к единице значения и по правилу округления приняты за 1.


Также в автом расчетах будут часто встречаться значения в экспоненциальной записи а Е - в 
Например, число 5,97е -15 означает 5,97 умножить на 10 в степени -15, где 5,97 число а и -15 число в.
Т.е очень приближенные к нулю значения.

Далее, когда уже есть расчеты и пв, и фр

Случайная величина в бином. распределении - кол-во раз.

В теорвере есть масса задач на неравенства,
т.е найти вероятность того, что случ. величина попадет в определенный интервал.
Например, в данном примере с ограничением 10 спинов, формулировка может быть такая:
Найти вероятность того, что номер повторится: 
менее 4-х раз,
не менее 3-х раз,
не более 3 раз,
более 2-х раз,
хотя бы 1раз,
более одного и не более 3-х раз
и др
 
Т.е здесь идет речь об интервалах

Менее 4-х раз - это когда х<4
вероятность (х<4) = p(0) + p(1) + p(2) + p(3)

Не менее 3-х раз - это когда х≥3
вероятность (х≥3) = 1- (p(0) + p(1) + p(2))
 
Не более 3-х раз - это когда х≤3
вероятность (х≤3)= p(0) + p(1) + p(2) + p(3)
или это f(3)

Более 2-х раз - это когда х >2
вероятность (х >2) = p(3) + p(4) + p(5) + p(6) + p(7) + p( + p(9) + p(10)

Хотя бы один раз - это когда х>0
вероятность (х>0) = 1- p(0)

Более одного и не более 3-х раз
Это двойное неравенство 1<х≤3
вероятность (1<х≤3) = р(2) + р(3)
или
f(3) - f(1)

Можно проверить:
р(2) + р(3) = 0,026400690087717 + 0,0019556066726416 = 0,02835629676
или
f(3) - f(1) = 0,99990169245113 - 0,97154539569077 = 0,2835629676
...
х=r

Далее, матем ожидание для биномиального распределения.

чуть исправлю 
Можно проверить:
р(2) + р(3) = 0,026400690087717 + 0,0019556066726416 = 0,02835629676
или
f(3) - f(1) = 0,99990169245113 - 0,97154539569077 = 0,02835629676