CMP - форум PRO игроков казино
Априорика от Виталика KWN (PARADOX выбора прогноза ставок)
- klick
-
 Автор темы
Автор темы
- expert
-

- Сообщений: 863
Априорика от Виталика KWN (PARADOX выбора прогноза ставок)
7 года 7 мес. назад - 4 года 1 мес. назадПрограмма PARADOX работает в режиме анализатора и способна до мелочей повторить результаты всего ранее сыгранного…
Не предназначена для «мультяшных» рулеток и адаптирована для игры с настоящим колесом и настоящим шариком. Не является конструктором для создания систем...
Применима к Пневмо-рулеткам и Live-рулеткам, в онлайн-казино.
Это не «указка выигрышных чисел», а инструмент для получения преимущества в долгую, в сумме серии игр, который при должном профессиональном отношении позволит получать доход в постоянной перспективе.
Наш сервис это всего лишь инструмент. Умение пользоваться этим инструментом взвешенно и уравновешенно, в конечном итоге определяет Вашу полезность. Если у Вас недостаточно средств, но Ваши качества и способности позволяют стать профессиональным игроком, то такой игрок всегда будет востребован.
:silly:
Взлом предлагаю совершить мозговым штурмом, ибо автор довольно болтлив :evil:
********************** модер.
Подумаем как улучшить программу-кликер-бот для рулетки от Casino Mining Pool

Для пользователей на платформе WIN32, WIN64 и Android лучшее это программа-кликер Roulette Mining:
100pravda.com/forum/statistic-program-ca...ki-kazino-pc-android
Улучшения алгоритмов прогноза ставок на рулетку, оптимальный БРМ и удобство только приветствуются. Поэтому не мешает изучать другие программы сторонних разработчиков, даже если они окажутся бесполезными калькуляторами и анализаторами игры в казино.
Пожалуйста Войти или Регистрация, чтобы присоединиться к беседе.
- klick
-
 Автор темы
Автор темы
- expert
-

- Сообщений: 863
Re: Априорика от Виталика KWN (PARADOX выбора прогноза ставок)
7 года 7 мес. назадКак только появится всплывающее окно, независимо от результатов - останавливаете игру. Игра закончена!
Суть игры по тактике «Троица» заложен, в её названии. Это три игровых подхода за сутки. В реальных играх, желательно три подхода к разным столам, что увеличивает шансы игрока не попасть, в слишком глубокий провал из серии игр с отрицательным результатом. Провалов, совсем избежать не удастся, но как показывает статистический анализ, на каждом отдельном столе, период отрицательных игр идёт серией и чтобы не попасть в эту серию, лучше сменить стол. (Детально можно рассмотреть в Таблице Excel, во вкладке: Результ.игр на одном столе+ГПСЧ).
Для тестовых уроков, для анализа, наоборот рекомендуем брать игры с одного стола, чтобы чётче и предметно прослеживалась динамика и хронология спадов и подъёмов. В нашем случаи, будем рассматривать игру по статистике стола: Playtech_live_(200000spin). Испытания "Троицей" проведенные на продолжительной статистике одного стола, наглядно показывают возникновение таких серий. Более того, можно поймать серии и из отрицательных серий, и на примере данной статистики, можно увидеть подобный участок начиная с 364, по 408 игру.
Три игровых подхода за игровой день - это аспект, из разряда психологических приёмов. Как правило, игрок ведёт подсчёт итогового баланса за день, воспринимая подходы к столам как часть единого игрового дня. Если из троицы, будет одна-две проигрышных и одна выигрышная игра, то она перекроет, или снизит проигрыш, и такой день будет восприниматься не таким провальным.
Пожалуйста Войти или Регистрация, чтобы присоединиться к беседе.
- klick
-
 Автор темы
Автор темы
- expert
-

- Сообщений: 863
Re: Априорика от Виталика KWN (PARADOX выбора прогноза ставок)
7 года 7 мес. назад - 7 года 7 мес. назадКогда игра закончится, дело случая и планово часик другой поиграть не удастся. Если ограничивать игру каким то фиксированным временем, или спешить во время игры, потому что завтра на работу, то это заведомо приведёт к суммарному поражению и никакая выигрышная стратегия тут не поможет.
Программа создана, чтобы нащупывать некую «парадоксальную» закономерность, которая всегда проявляется в случайном. Её трудно поймать, но если удаётся, то удастся и использовать.
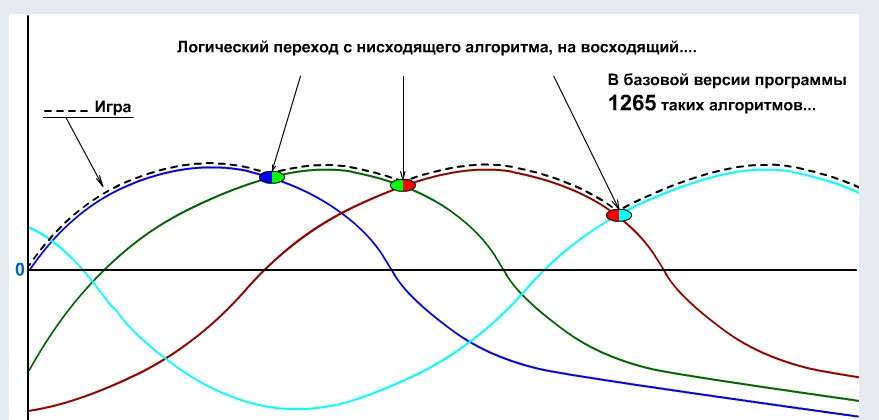
Статистические показатели: после достижения "зелёного окна", нащупанный роботом алгоритм, ещё будет играть в плюс, в 70-80% случаях.
Тактики выжидания дают ещё одно преимущество. Автомат не всегда продуктивен, но если его применять только для нащупывания зелёного окна, без ставок, а значит и без риска. То, какая бы фатальная рулетка, для игрой автоматом не попалась, игра с ней состоится только в случаи, если удастся нащупать эффективный алгоритм, что резко увеличивает шансы не остаться в проигрыше.
Статистический анализ, как раз показывает, что существуют очень протяженные по дням участки, когда алгоритм не выходит на зелёное окно а, следовательно, либо болтается по нулям, либо проигрывает.
<чистосердечное признание :evil: >
Пожалуйста Войти или Регистрация, чтобы присоединиться к беседе.
- klick
-
 Автор темы
Автор темы
- expert
-

- Сообщений: 863
Re: Априорика от Виталика KWN (PARADOX выбора прогноза ставок)
7 года 7 мес. назадАвтоматический режим, в среднем выигрывает 55 игр, из 100 сыгранных.
:evil:
Светофор - табло из двенадцати чисел в три ряда. По четыре числа на каждый ряд. В этом табло отображаются прогнозируемые числа, на которые нужно сделать в данный момент ставку. По одному «Анте» на каждое число. Если фон, под какими-либо из чисел окрасился цветом, это значит, что это число отображается в светофоре несколько раз. Сколько раз число отображается, столько «анте» на него и ставите. Это не увеличение ставок в прогрессии – это означает, что алгоритмы сошлись на том, что это число выпадет вероятнее всего и ставку надо усилить.
Пожалуйста Войти или Регистрация, чтобы присоединиться к беседе.
- klick
-
 Автор темы
Автор темы
- expert
-

- Сообщений: 863
Re: Априорика от Виталика KWN (PARADOX выбора прогноза ставок)
7 года 7 мес. назад:evil:
Представьте, что за игровым столом сразу играют тысячи игроков - причём каждый по-своему, и Вы пристраиваетесь ставками к самому успешному. В основе алгоритмов лежит сложная адаптивная система, но у каждого алгоритма своя логика действий, которая, в свою очередь, адаптируется и меняется в зависимости от набора статистических данных (последовательности чисел выпавших на рулетке). В остальном Вы, конечно, можете попытаться понять логику ставок, которую предлагает тот или иной алгоритм, но в какой-то момент ставки будут на одни и те же числа, в другой момент числа могут меняться, чуть ли не каждый спин. Так как мы отслеживаем случайность, то и в результате, всё что делает система, будет сильно напоминать случайность. Если нет ниточки, за которую надо потянуть, то и происходящее будет непостижимо.
:evil: Ничего не напоминает со старого casino-mining.com ?!
Пожалуйста Войти или Регистрация, чтобы присоединиться к беседе.
- klick
-
 Автор темы
Автор темы
- expert
-

- Сообщений: 863
Re: Априорика от Виталика KWN (PARADOX выбора прогноза ставок)
7 года 7 мес. назад2+2х2=?
Если не учесть правила сложения и умножения, то получится восемь.
Сравнение с этим нехитрым примером показывает, что упуская некоторые обстоятельства, любую задачу можно трактовать неверно.
Кто ни будь, задавался вопросом, что в решении - Можно ли обыграть рулетку? - изначально неправильно истолковывается и формулируется задача?
Начнём с того, что «серьёзные» люди не обсуждают. С полной бессмыслицы. С закона «Двух третей», звучит он так:
За 37-мь спинов, из 37-ми чисел на рулетке сыграет, только две трети этих чисел.
Кто-то эту закономерность законом не считает, полагая чем-то вроде «следствия» но, сколько шарик не пускай этот закон силой мысли не изменишь, разве что, на досуге раздолбав колесо рулетки молотком. Но мы не экстремалы, посему пойдём путём согласия и непротивления, и примем его как данность, назвав не законом, а закономерностью…
Назовём её, закономерностью всех замкнутых систем, ярким представителем коих и является игра «Рулетка». Чисел ровно 37-мь, не убавится, не добавится – процессы замкнуты, в единый цикл с равновероятным исходом.
Копну ещё глубже. Закономерность «Двух третей» это вселенское правило, делающее случай - случайным. Выпадай на рулетке за 37-мь спинов, все 37-мь чисел, то чтобы выигрывать, было бы достаточно, делать ставки на числа, которые ещё не сыграли. Или, выпадай за 37-мь спинов всего одна вторая от имеющихся чисел, достаточно было бы делать ставки на числа, которые уже сыграли по разу.
В обоих вариантах – рулетка превратилась бы, в последовательную систему, которую можно легко предсказать. Отсюда «две трети» для непредсказуемости случая – это в самый раз.
Теперь, в чём интрига?
Была сформулирована задача:
За игровым столом 37 игроков
У каждого игрока 37 фишек
Каждый игрок, каждый спин, делает ставку только на одно число, по одной фишке.
У каждого игрока своё число, на весь период игры и другие числа игрок не ставит.
(Рулетка 37-мь чисел, каждому игроку по числу)
Игра длиться всего 37 спинов.
Вопросы:
Сколько в среднем игроков по завершению игры останется, в проигрыше?
Сколько в среднем игроков проиграет полностью?
Сколько в среднем игроков выиграет больше, чем проиграет?
Задача не с подвохом, а скорее прелюдия, чтобы описать суть теории. Предлагаю решить задачку, поменяв в ней приоритеты, расширив трактовку обсуждаемой закономерности.
Закономерность «Двух третей» - не о том, что за 37-мь спинов выпадет всего две трети чисел. Она о том, что треть чисел не сыграет потому что, будет вытеснена повторами.
Чтобы получить средний результат - после расчёта двух третей, выводим точное количество не сыгравших чисел, а следовательно получим ровно такое же количество повторов. Повтор примем за единицу измерения и произведём с полученным количеством дополнительный расчёт. Допустив условие, что в этом количестве срабатывает всё та же закономерность «Двух третей». По факту мы имеем закономерность, в закономерности.
Вычисленная сумма повторов будет образовывать, тоже две трети чисел и одна треть будет вытеснена уже повторами-повторов этих чисел. К примеру: если было 12-ть повторов, то чисел в этой дюжине, будет всего восемь, часть из которых сыграет трижды-четырежды.
Теперь вернёмся к осмыслению задачи:
Из 37-ми игроков, по итогам игры длинною в 37-мь спинов, у нас должно получиться три группы и в задаче нужно определить количество игроков, в каждой из этих групп (по факту мы подсчитываем не игроков, а рассчитываем числа).
Выпадение чисел на рулетке равновероятно, следовательно, и формирование групп равновероятно. И в идеальной модели, в ответе, мы должны получить две равновероятные группы проигравших, и одну группу выигравших с поправкой на «закономерность, в закономерности» – группа выигравших должна быть равна двум третям от количества группы проигравших.
Вышло что-то вроде «популярной механики» но, не смотря на то, что многие посчитают это определение бесполезным, оно спрятало в себе ещё одно заключение: Имея средний результат, в нём видим, что закон «Двух третей» не имеет ни чего общего с тем, что на рулетке за цикл в 37-мь спинов выпадет две трети чисел и их будет меньше. Зато за данный цикл произойдет больше «повторов», и их будет больше одной трети (внимание: «повторов», а не повторившихся чисел).
Если вернёмся к тому, что я писал в начале: что, «две трети» это вселенское правило, делающее случай – случайным. Будь в замкнутой системе перевес в одну, или другую сторону, мы получим последовательную систему, а не случайную. И мы получаем этот «Парадокс»: если будем следовать ставками не за числами (подчёркиваю: не за числами), а за «повторами»* мы получим хоть и не значительный, но перевес. И наоборот, мы окажемся в более проигрышном положении, если будем делать ставки на числа, которые не выпадали.
*Как следовать за «повторами»? - это уже другой разговор об ещё одной закономерности, но сразу оговорюсь, что к «горячим числам», которые так любят публиковать в своей статистике казино, это тоже не имеет никакого отношения.
Для общей ясности, добавлю: Повторы не привязаны к номерам, каждый новый спин меняются кандидаты (номера), и номера на которые делается ставка, возможно ещё не разу и не повторялись, но характерный повтор уже происходил и стабильно происходит. И надо прогнозировать повтор, а какое это число будет, это уже как на него повтор ляжет (Это упрощение, но по сути близко к оригиналу.)
С уважением,
Виталий Квинстар
Пожалуйста Войти или Регистрация, чтобы присоединиться к беседе.
Работай над своей Удачей!
Игра в казино: все мы учимся на пробах и ошибках. Наша цель - свести к минимуму затраты на этом пути и улучшить финансовые результаты. Эксперты CMP тщательно протестировали каждый аспект работы на реальных деньгах в разных казино. Форум помогает всем игрокам экономить деньги и время. Изучите лучшие игровые стратегии и основные инструменты (включая мобильные приложения). Вы получаете важные идеи для победы над казино и уменьшаете свои потери. Присоединяйтесь, чтобы ускорить и упростить свой путь к PRO игре в казино!

Copyright © 2011-2024 ESPT GO LIMITED Reg. : HE 370907
Vasili Michailidi, 9, 3026, Limassol, Cyprus, phone: +35796363497