CMP - форум PRO игроков казино
Смелая и осторожная игра (теория вероятности)
- DLK
-
 Автор темы
Автор темы
- moder
-

- Сообщений: 2500
Смелая и осторожная игра (теория вероятности)
4 года 11 мес. назад - 4 года 11 мес. назадЧеловеку, находящемуся в Лас-Вегасе, нужны 40 долларов, в то время как он располагает лишь 20 долларами. Он не хочет телеграфировать жене о переводе денег и решает играть в рулетку (отрицательно относясь к этой игре) согласно одной из двух стратегий:
▪ Поставить все свои 20 долларов на «чет» и закончить игру сразу же, если он выиграет или проиграет.
▪ Ставить на «чет» по одному доллару до тех пор, пока он не выиграет или не проиграет 20 долларов.
Какая из этих двух стратегий лучше?
Решение задачи
Еще одна задача на случайные блуждания с поглощением. Её решение приведено не полностью, а как продолжение ранее рассмотренных задач.
"Смелая игра", т. е. ставка 20 долларов сразу, дает игроку вероятность выигрыша равную 18/38 ≈ 0.474. Вычисление вероятности выигрыша при осторожной игре по доллару за одну партию сводится к задаче о разорении игрока со следующими параметрами:
первоначальный капитал 1-го игрока: m = 20;
первоначальный капитал 1-го игрока: n = 20;
вероятность удачного исхода в отдельной игре: p = 18/38;
вероятность неудачного исхода (проигрыша) в отдельной игре: q =1 - 18/38 = 20/38.
Подставляя эти значения в формулу для вероятности выигрыша M, получаем
P = [1 - (p/q)m] / [1 - (p/q)m+n] = [1 - (20/18)20] / [1 - (20/18)40] = [1 - 8.23] / [1 - 67.65] ≈ 0.108.
Итак, "осторожная игра" уменьшает шансы игрока на выигрыш вчетверо по сравнению со "смелой игрой".
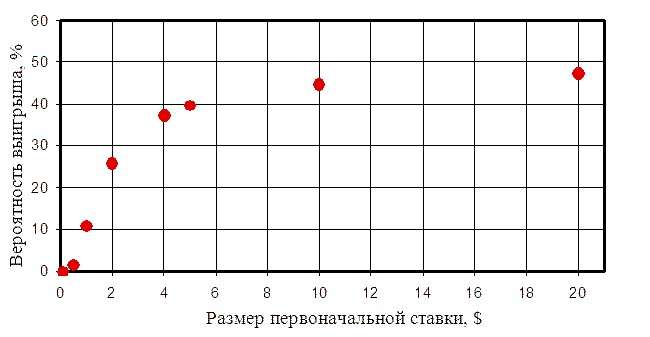
К чему приводят случайные блуждания: снижение вероятности выигрыша при дроблении ставок
Интуитивное объяснение этого явления состоит в том, что смелая игра есть также быстрая игра.
Впрочем, мы видели, что интуиция, основанная на средних, не всегда ведет к правильным выводам о вероятностях. Дубинс и Сэвидж замечают, что им неизвестно доказательство, основанное на подобных интуитивных рассуждениях. Однако в нашем специальном случае удвоения начальной суммы при игре в «красное и черное» нижеследующие пояснения Сэвиджа основываются именно на этой идее.Быстрая игра сокращает время игры против казино, которая не является безобидной.
Подготавливая эти пояснения об игре в казино Сэвидж сознательно опустил некоторые математические тонкости, касающиеся случая равенств в неравенствах для вероятностей.
«Золотой рай»
В «Золотом раю» можно играть в любую безобидную игру, если только игрок располагает достаточным начальным капиталом. Игрок, входящий в «Золотой рай» с x долларами и желающий получить доход в y долларов, может достигнуть своей цели с вероятностью x/(x + y), поставив все свое достояние x на единственный шанс выиграть y долларов с вероятностью x/(x + y), что является, очевидно, безобидной игрой. Как известно, никакая стратегия не дает большей вероятности выигрыша, и вероятность выигрыша максимальна тогда и только тогда, когда играющий заведомо либо проигрывает x либо выигрывает y долларов.
«Меньший рай»
«Меньший рай» походит на «Золотой рай», но с той существенной разницей, что, покидая игорный зал, игрок должен уплатить налог размером t (0 < t < 1) с любой положительной суммы, которую он приобрел во время игры. Поэтому для играющего не труднее и не легче выиграть y с начальным капиталом в x долларов, чем игроку в «Золотом раю» выиграть y / (1 - t) долларов. Наибольшая вероятность, с которой он может достигнуть цели, равна поэтому
Pmax = [(1 - t) • x] / [(1 - t) • x + y].
«Потерянный рай»
Здесь крупье собирает налог размером t от положительного дохода, если он есть, после каждой сыгранной партии. В этом случае игрок, очевидно, находится не в лучших условиях, чем его собрат в «Меньшем раю». В частности, (1) есть верхняя граница для вероятности выиграть y долларов с начальным капиталом x в «Потерянном раю». Эта вероятность может быть достигнута при ставке всего капитала в одной партии, как и прежде. Однако указанная вероятность не может быть получена ни при какой стратегии, для которой вероятность выигрыша любой положительной суммы, меньшей чем y (после выплаты налогов), положительна. Чтобы убедиться в этом, заметим, что игрок в «Меньшем раю» может имитировать любую стратегию игрока из «Потерянного рая», откладывая после каждой партии ту сумму, которую отбирает крупье от игрока из «Потерянного рая». Таким образом, первый игрок может иметь больший ожидаемый доход, чем второй игрок при любой стратегии, в которой вероятность выигрыша любой положительной суммы, меньшей у, положительна.
«Красное и черное»
В «Красном и черном» игрок может поставить любую сумму в игре с вероятностью w (0 < w < 1/2) выигрыша, равного его ставке. Иначе говоря, он выигрывает то, что полагалось бы при безобидной игре с (1 - w)/w своей ставки, и затем уплачивает налог, равный t, где
t = (1 - 2w) / (1 - w).
Поэтому вероятность для игрока в «Красное и черное» выиграть y долларов с начальным достоянием в x долларов не превосходит (1), так же как и для игрока в «Потерянном раю». В терминах величины w эта верхняя грань равна
w•x / [w•x + (1 - w)•y].
Более того, значение может быть достигнуто только в том случае, когда вероятность выиграть положительную сумму, меньшую, чем y, в отдельных играх равна нулю. Причем заведомо игрок либо проигрывает ровно x долларов, либо выигрывает ровно y. Можно показать, что эта ситуация осуществляется только тогда, когда y = x, и игрок участвует только в одной смелой игре с вероятностью выигрыша w, определяемой из (2), суммы в y долларов.
Задача об отыскании точных верхних границ и оптимальных стратегий для игрока в «Красное и черное», который хочет выиграть сумму, отличную от x, более трудна.
Пожалуйста Войти или Регистрация, чтобы присоединиться к беседе.
- Coin
-

- moder
-

- ☜♡☞ Roulette foreva ☜♡☞
- Сообщений: 893
Re: Смелая и осторожная игра (теория вероятности)
4 года 11 мес. назадПожалуйста Войти или Регистрация, чтобы присоединиться к беседе.
Работай над своей Удачей!
Игра в казино: все мы учимся на пробах и ошибках. Наша цель - свести к минимуму затраты на этом пути и улучшить финансовые результаты. Эксперты CMP тщательно протестировали каждый аспект работы на реальных деньгах в разных казино. Форум помогает всем игрокам экономить деньги и время. Изучите лучшие игровые стратегии и основные инструменты (включая мобильные приложения). Вы получаете важные идеи для победы над казино и уменьшаете свои потери. Присоединяйтесь, чтобы ускорить и упростить свой путь к PRO игре в казино!

Copyright © 2011-2024 ESPT GO LIMITED Reg. : HE 370907
Vasili Michailidi, 9, 3026, Limassol, Cyprus, phone: +35796363497