Дискретные распределения (Alatissa эксперт по теории вероятности)

Далее, когда уже есть расчеты и пв, и фр

Случайная величина в бином. распределении - кол-во раз.

В теорвере есть масса задач на неравенства,
т.е найти вероятность того, что случ. величина попадет в определенный интервал.
Например, в данном примере с ограничением 10 спинов, формулировка может быть такая:
Найти вероятность того, что номер повторится: 
менее 4-х раз,
не менее 3-х раз,
не более 3 раз,
более 2-х раз,
хотя бы 1раз,
более одного и не более 3-х раз
и др
 
Т.е здесь идет речь об интервалах

Менее 4-х раз - это когда х<4
вероятность (х<4) = p(0) + p(1) + p(2) + p(3)

Не менее 3-х раз - это когда х≥3
вероятность (х≥3) = 1- (p(0) + p(1) + p(2))
 
Не более 3-х раз - это когда х≤3
вероятность (х≤3)= p(0) + p(1) + p(2) + p(3)
или это f(3)

Более 2-х раз - это когда х >2
вероятность (х >2) = p(3) + p(4) + p(5) + p(6) + p(7) + p( + p(9) + p(10)

Хотя бы один раз - это когда х>0
вероятность (х>0) = 1- p(0)

Более одного и не более 3-х раз
Это двойное неравенство 1<х≤3
вероятность (1<х≤3) = р(2) + р(3)
или
f(3) - f(1)

Можно проверить:
р(2) + р(3) = 0,026400690087717 + 0,0019556066726416 = 0,02835629676
или
f(3) - f(1) = 0,99990169245113 - 0,97154539569077 = 0,2835629676
...
х=r

Далее, матем ожидание для биномиального распределения.

чуть исправлю 
Можно проверить:
р(2) + р(3) = 0,026400690087717 + 0,0019556066726416 = 0,02835629676
или
f(3) - f(1) = 0,99990169245113 - 0,97154539569077 = 0,02835629676

Прежде чем перейти к полиномиальному распределению, еще более подробно про биномиальное.

Например,
10 спинов
для номера 7
... 30, 26, 14, 32, 00, 32, 17, 28, 35, 24 - ни разу №7
...13, 20, 19, 18, 15, 07, 27, 34, 24, 11 - один раз №7
...32, 17, 07, 35, 12, 07, 27, 24, 10, 05 - два раза №7
...23, 07, 12, 07, 14, 35, 20, 07, 24, 05 - три раза №7
...20, 07, 14, 07, 19, 07, 34, 07, 21, 24 - четыре раза №7
и т.д. 

Среднее кол-во раз  можно узнать по спец формуле мат ожидания для бином распределения.

Мат ожидание - это среднеожидаемое знач случ величины, ( в данном распределении это кол-во раз).
M=np
для 10 спинов 
10* 1/37≈  0,27027027
округление 0
значит в среднем ни разу.

для 100 спинов 
100* 1/37 ≈ 2,7027027027
округление 3
в среднем 3 раза.

Про мат ожидание говорили в других темах
100pravda.com/forum/roulette-game/715-vy...zhov?start=120#25742

Внесу-ка и я свои 5 коп. Насчет вероятностей, баланса и РОИ.
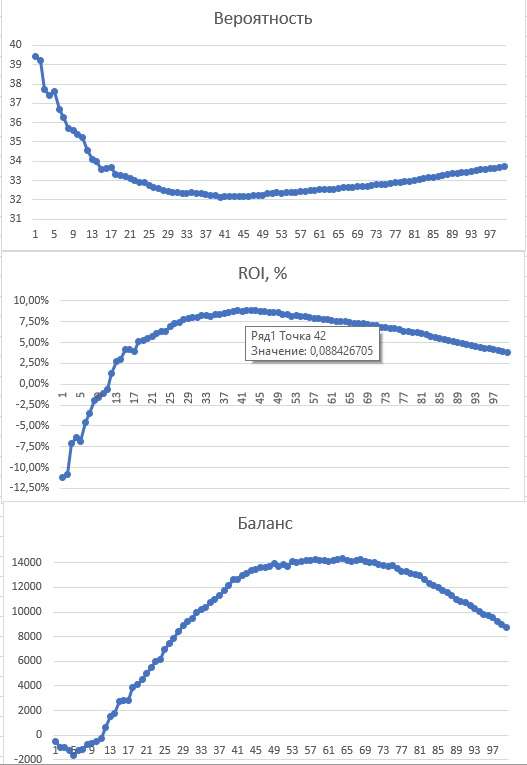
Эти 3 графика созданы для схемы, основанной на одной моей как бы теории. Саму теорию излагать не буду, схему тоже.  Просто графики показывают, что самое высокое РОИ не означает самый большой баланс. И наоборот. 

Схема опробована на 40К спинах. Не факт, что она вообще правильная, при расчетах в Excel я много раз наступал на одни и те же грабли. Вроде все шоколадно, а в логике или расчетах ошибка. Но речь не о том. 
Взял 100 параметров от 1 до 100, это по сути максимальное количество спинов, в течение которых ставим на номер, начиная с определенной точки (их может быть и меньше в зависимости от некоторых критериев). Получил 3 графика:



1. Вероятность (эмпирическая, т.е. относительная частота угадывания). На графике она в виде знаменателя дроби типа 1/37
2. ROI
3. Баланс

Как видно, макс. вероятность получается для точки 42 (ставка на номер не более 42 спина подряд), она равна 1 / 32,1565. В этой же точке и максимальное ROI = 0,088 т.е. 8,8%. Но абсолютный баланс в этой точке далеко не максимальный (12976 фишек). А максимальный баланс 14378 в точке 64, в которой ROI = 0,0756, а вероятность 1 / 32,53 (ниже, чем для точки 42).

Интересно мнение, что лучше: играть с максимальным балансом или с макс. ROI ?